In this post, we will use deep learning to build a simple model that can automatically detect potholes in images of roads.
Detecting and fixing potholes is an important aspect of public road maintenance; left unchecked, they can cause major damage to vehicles and have long-term economic consequences. Studies show that the South African government spent over R22 billion over the past 3 years on pothole repair programs. Potholes also pose a serious danger to motorists, but manually identifying can be a daunting task and a time-consuming exercise.
Datasets
A bit of background about the dataset: the MIIA Pothole Image Classification Challenge was designed for Leaderex and AI Expo, taking place on 3 and 4 September 2019, respectively. The data contains images of streets in South Africa that either have potholes or do not. The data is split into a test and train set; the training set contains 4,026 images, while the test set contains 1,650 images. The data can be found here. This is a knowledge competition which means it stays open permanently and anyone can try it.
Model
For this problem, we will build a Convolution Neural Network (CNN) using a Jupyter notebook. We will upload the images and train them. The images are in RGB (Red, Green, Blue) format; you can read more about RGB here.
For the steps below, follow along with my code on Github.
Image labeling
The data is divided into two folders, one for training and the other for testing. The training folder contains the training images which we will use to train the model.
We will create a vector to hold the training images. We use the load_img function from numpy to import the images into the Jupyter environment. The load_img converts the RGB images into numbers between 0 and 255. We use a for-loop to mark each image using their image id and format. We then append the images onto each other and store them in an array. The code snippet will create the above-mentioned process.
# We have grayscale images, so while loading the images we will keep grayscale=True, # if you have RGB images, you should set grayscale as false train_image = [] for i in tqdm(range(train.shape[0])): img = image.load_img(train['image_ID'][i]+'.JPG', target_size=(28,28,1), grayscale=False) img = image.img_to_array(img) img = img/255 train_img.append(img) X = np.array(train_image)
Apply transformations
After storing the training images into a vector, we split them in two sets by using the 20/80 rule. We will use 80 percent of the images to train the model and the other 20 percent to test it.
Now we set up the convolutional neural network (CNN). Since we are building the CNN from scratch we need to specify a few parameters associated with the model. We specify the input shape to be the same size as the vector holding the images. For the pooling layer we use a size of 2. The dropout is 0.25 and for the activation function we use a softmax.
model = Sequential() model.add(Conv2D(32, kernel_size=(3, 3),activation='relu',input_shape=(28,28,1))) model.add(Conv2D(64, (3, 3), activation='relu')) model.add(MaxPoolong2D(pool_size=2, 2))) model.add(Dropout(0.25)) model.add(Flatten()) model.add(Dense(128, activation='relu')) model.add(Dropout(0.5)) model.add(Dense(10, activation='softmax'))
The architecture of the CCN is shown below.
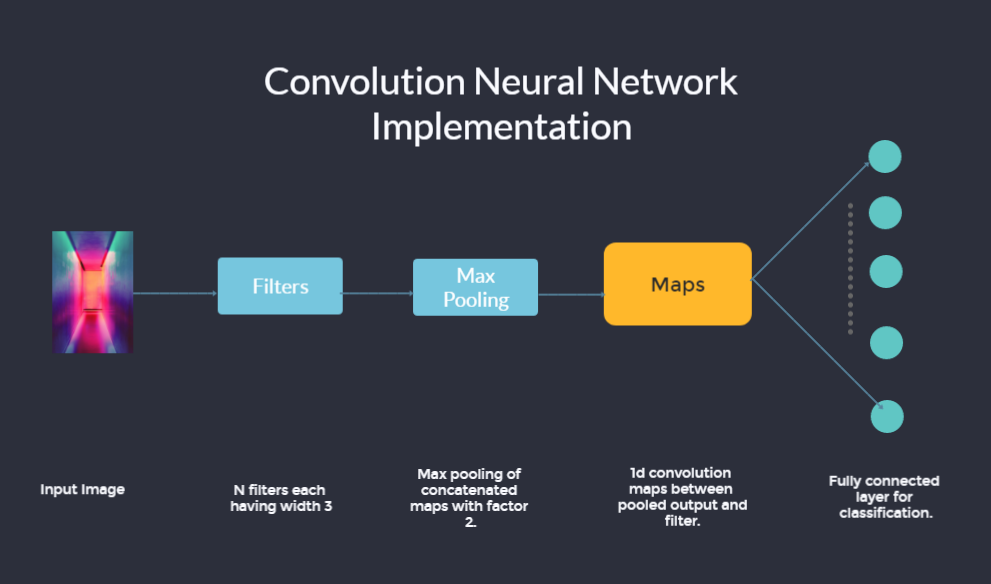
Model training
We train the model by using an Adam optimiser, and set the epochs to 10. For the objective function we use a ‘sparse categorical cross-entropy’ and we set our metric to accuracy since we’re interested in measuring the log loss of the model. Logarithmic loss (related to cross-entropy) measures the performance of a classification model where the prediction input is a probability value between 0 and 1. You can read more about log loss here. After defining those parameters, we fit the model on the training data.
model.compile(loss='sparse_categorical_crossentropy, optimizer='Adam',metrics=['accuracy']) model.fit(X_train, y_train,epochs=10)
Epoch 1/10 3220/3220 [==============================] - 7s 2ms/step - loss: 0.4589 - acc: 0.7870 Epoch 2/10 3220/3220 [==============================] - 7s 2ms/step - loss: 0.3132 - acc: 0.8618 Epoch 3/10 3220/3220 [==============================] - 7s 2ms/step - loss: 0. 2594 - acc: 0.8910 Epoch 4/10 3220/3220 [==============================] - 7s 2ms/step - loss: 0.2341 - acc: 0.8994 Epoch 5/10 3220/3220 [==============================] - 7s 2ms/step - loss: 0.2005 - acc: 0.9168 Epoch 6/10 3220/3220 [==============================] - 7s 2ms/step - loss: 0.1740 - acc: 0.9326 Epoch 7/10 3220/3220 [==============================] - 7s 2ms/step - loss: 0.1482 - acc: 0.9407 Epoch 8/10 3220/3220 [==============================] - 7s 2ms/step - loss: 0.1458 - acc: 0.9422 Epoch 9/10 3220/3220 [==============================] - 7s 2ms/step - loss: 0.1208 - acc: 0.9559 Epoch 10/10 3220/3220 [==============================] - 7s 2ms/step - loss: 0.1264 - acc: 0.9506
Prediction on images
We now apply the model on the test data, this is data the model has never interacted with. The unseen images are 1,650 images. This is the most interesting part, as we now get to see how the model performs.
y_score = model.predict_proba(X_test)
print(y_score)
[[9.8533183e-01 1.4668099e-02]
[9.9933630e-01 4.0945363e-01
...
[7.5465256e-01 2.4534738e-01]
[3.3280409e-03 9.9667192e-01]
[7.4173373e-01 2.5826630e-01]]
test = pd.read_csv('test_ids_only.csv')
Saving the results in a text file.
np.savetxt("sample.csv",sample_submission,deliiter = ",")
Using the clip function to improve the log loss.
sample_submission1 = model.predict_proba(Test).clip(0.1,0.3)
Saving the results in a text file.
np.savetxt("sample.csv",sample_submission1,delimiter = ",")The model handled the image quite well. Remember the objective was to detect potholes in an image with high accuracy. The log loss of the model is good. To improve the model further we can use the clip function. This function maximizes the log loss of the model. The log was 1.43 but using the clip function the log loss is at 0.65.
Summary
I have shown here how easily you can build CNNs and apply them to real-world applications. All this was achieved using open-source tools, and it only took a few hours to compile this solution.
About the author
Blessing Magabane is a full stack data scientist at Altron Bytes Managed Solutions (LinkedIn | Zindi | GitHub). He is passionate about data science and solving problems using machine learning. For collaboration on data science projects, please get in touch with him via LinkedIn.