Lacuna - Correct Field Detection Challenge
This is based on ZzyZx asking some questions in another thread. I thought to start this discussion to address general questions, typically like those ZzyZx asked.
Note!
This is not in any way an official discussion and I am not affiliated with Zindi or Lacuna or anybody else that may have something to do with this. In fact, I am a competitor just like you who, in reality, wants to beat you in this competition.
That said, I also do this to learn and grow and what better way to share and check results, so this is really for that. This is also to generate some chatter that everybody can use to their own benefit.
I hope others will join in and help in answering common questions but you are responsible for guarding your own solutions while helping others.
Herewith a first one. ZzyZx asks
We are predicting displacement vectors. The GPS is not known. This should be obvious.
You can either predict the displacement vector directly or convert to pixels and project the displacement in pixels. The model you use will determine which will be better for you.
The formula in the starter notebook shows you how to convert the vector to pixels. Note that you need to find the center first. Here is my utility functions that convert from the vector to pixels and back.
# Get image center in image pixels
def img_center_loc ( img ):
return img.shape [ 1 ] // 2, img.shape [ 0 ] // 2
# Given an image and target coordinates, return the target location in image pixels
def img_target_loc ( img, tgtx, tgty ):
ctr = img_center_loc ( img )
x1 = ctr [ 0 ] - np.round ( tgtx / CONST_X * img.shape [ 1 ] )
y1 = ctr [ 1 ] + np.round ( tgty / CONST_Y * img.shape [ 0 ] )
return int ( x1 ), int ( y1 )
# Given an image and target coordinates, return the target location in image pixels
def img_target_loc_with_ctr ( img, tgtx, tgty, ctr ):
x1 = ctr [ 0 ] - np.round ( tgtx / CONST_X * img.shape [ 1 ] )
y1 = ctr [ 1 ] + np.round ( tgty / CONST_Y * img.shape [ 0 ] )
return int ( x1 ), int ( y1 )
# Given an image and image location in pixels, return the target coordinates
def img_loc_coords ( img, pixx, pixy ):
ctr = img_center_loc ( img )
x = CONST_X * float ( ctr [ 0 ] - pixx ) / float ( img.shape [ 1 ] )
y = CONST_Y * float ( pixy - ctr [ 1 ] ) / float ( img.shape [ 0 ] )
return x, y
# Given an image, the image center and some location in pixels, return the target coordinates
def img_loc_coords_with_ctr ( img, pixx, pixy, ctr ):
x = CONST_X * float ( ctr [ 0 ] - pixx ) / float ( img.shape [ 1 ] )
y = CONST_Y * float ( pixy - ctr [ 1 ] ) / float ( img.shape [ 0 ] )
return x, y
The forward is given in the starter and the backward you should be able to work out with pen and paper easily. You can easily make a mistake as well, so double check that and let me know if you have issues with it.
To get the center you need the formula - see the code above. The point constants
CONST_X = 10.986328125 / 2
CONST_Y = 10.985731758 / 2
are used, *I assume*, to convert from pixels to meters and I think is some kind of an average that the organisers got from their own data. It is just a scaling issue so any good model should be able to handle it easily. I mean, if you predict meters or feet (or pixels), it is the same thing, just in different scales. There is of course some rounding at play, especially at the pixel level, and I suspect this will in fact pollute your model, and for purity in the extreme you should perhaps address it by adding or subtracting a 0.5 here or there, but I doubt at this stage that pursuing this is relevant or productive in any way.
FWIW there have been times when I thought surely, the scaling used is wrong. When visually inspecting the images I would often think the field lies on the opposite side of some cardinal or that the vector needs to be doubled in the same direction to hit the field center. I've tried a few times to change these constants but nothing seems to work universally, so for now let us just assume they are correct as given and applied correctly as in the starter examples (on which the snippet above is based).
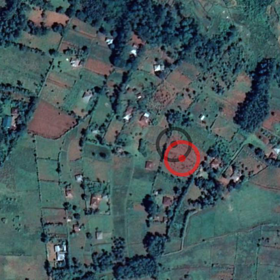
This is what makes this particular challenge so difficult - it is nearly impossible to correctly identify the field center using the images we have, so how do we get the machine to do so?
You know how sometimes something sticks with you ... ever since writing above
this issue has been bugging me. Now to continue this discussion I need to be able to draw some pictures and so I did it here (bottom of page). In summary, if you have the perfect model and get the plot centres accurate to the pixel level, you will still have an MAE of 0.015! If you improve to accurate to 0.5 a pixel then your MAE will drop to 0.008.